流体动力学问题剖析
发布日期: 2018-4-12
本节主要讨论流体在运动时的运动规律、能量转换以及运动流体对固体壁面的作用力和发作用力等问题,具体要介绍三个基本方程式及连续方程、能量方程和动量方程。
不过对液压技术来说,让人感兴趣的应该是整个流体在空间某特定点处或特定区域内的平均运动情况。此外,运动流体的状态还与流体的温度、粘度等参数都有联系。为了简化条件便于分析,一般都假设在等温的条件下(因而可把粘度看作是常量,密度只与压强有关)来讨论流体的运动情况。
一、基础概念
在推导流体运动的三个基本方程之前,必须弄清有关流体运动时的一些主要基础概念。
(一)理想流体、恒定运动和一维运动实际流体体具有粘性,研究流体运动时必须考虑粘性的影响。但由于这个问题很复杂,所以开始分析时可以假设流体体没有粘性,然后再考虑粘性的作用并通过实验验证等办法对理想化的结论进行补充或修正。这种方法同样可以用来处理流体的可压缩性问题。一般把既无粘性又不可压缩的假想流体称为理想流体。
流体运动时,如流体中任何一点的压强、速度和密度都不随时间而变化,便称流体是在作恒定运动;反之,只要压强、速度或密度中有一个参数随时间变化,则流体的运动被称为非恒定运动。研究液压系统稳态性能时,可以认为流体作恒定运动;但在研究其动态性能时,则必须按非恒定运动来考虑。
当流体整个作线形运动时,称为一维运动;当作平面或空间运动时,称为二维或三维运动。一维运动最简单,但是严格意义上的一维运动要求液流截面上各点处的速度矢量完全相同,这种情况在现实中极为少见。通常把封闭容器内流体的运动按一维运动处理,再用实验数据来修正其结果,液压传动中对工作介质运动的分析讨论就是这样进行的。
(二)流线、流管和流束
流线是流场中的一条条曲线,它表示在同一瞬时流场中各质点的运动状态。流线上每一质点的速度向量与这条曲线相切,因此,流线代表了某一瞬时一群流体质点的流速方向,如下图1-1所示。在非恒定运动时,由于液流通过空间点的速度随时间变化,因而流线形状也随时间变化;在恒定运动时,流线形状不随时间变化。由于流场中每一质点在每一瞬时只能有一个速度,所以流线之间不可能相交,流线也不可能突然转折,它只能是一条光滑的曲线。
在流场中画一不属于流线的任意封闭曲线,沿该封闭曲线上的每一点作流线,由这些流线组成的表面称为
如图1-1流线、流管、流束和通流截面
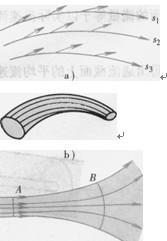
a)流线b)流管c)流束和通流截面
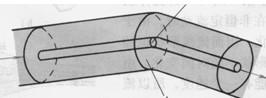
流管(见图1-2b)。流管内的流线群称为流束。根据流线不会相交的性质,流管内外的流线均不会穿越流管,故流管与真实管道相似。将流管截面无限缩小趋近于零,便获得微小流管或微小流束。微小流束截面上各点处的流速可以认为是相等的。
流线彼此平行的运动称为平行运动;流线间夹角很小,或流线曲率半径很大的运动称为缓变运动。平行运动和缓变运动都可以算是一维运动。
(三)通流截面、流量和平均流速
流束中与所有流线正交的截面称为通流截面,如图1-2c中的A面和曰面,通流截面上每点处的运动速度都垂直于这个面。
单位时间内流过某通流截面的流体体积称为流量,常用g表示,即
Q=V/T
式中q-流量,在液压传动中流量常用单位为L/min;
V—一流体的体积;
T——流过流体体积y所需的时间。
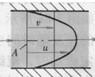
由于实际流体具有粘性,因此流体在管道内运动时,通流截面上各点的流速是不相等的。管壁处的流速为零,管道中心处流速最大,流速分布。若欲求得流经整个通流截面A的流量,可在通流截面A上取一微小流束的截面dA,则通过dA的微小流量为
dq=udA
对上式进行积分,便可得到流经整个通流截面A的流量
q= udA
可见,要求得g的值,必须先知道流速M在整个通流截面A上的分布规律。实际上这是比较困难的,因为粘性流体流速M在管道中的分布规律是很复杂的。所以,为方便起见,在液压传动中常采用一个假想的平均流速来求流量,并认为流体以平均流速流经通流截面的流量等于以实际流速流过的流量,即
q= udA= vA
由此得出通流截面上的平均流速为
v=q/a


a) b)
流量也可以 用单位时间内流过某通流截面的流体质量来表示,即dq。=pudA及g。=
f pMdA,g。称为质量流量。
oA
(四)运动流体的压强
静止流体内任意点处的压强在各个方向上都是相等的;可是在运动流体内,由于惯性力和粘性力的影响,任意点处在各个方向上的压强并不相等,但在数值上相差甚微。当惯性力很小,且把流体当作理想流体时,运动流体内任意点处的压强在各个方向上的数值仍可以看作是相等的。